| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- 객체 탐지
- VOC 변환
- InstructPix2Pix
- 논문 분석
- Carla
- Custom Animation
- 논문분석
- Paper Analysis
- object detection
- 리눅스 빌드
- DOTA dataset
- AI Security
- 커스텀 애니메이션 적용
- Linux build
- TensorFlow Object Detection API install
- 크롤링
- Branch 활용 개발
- Object Detection Dataset 생성
- Towards Deep Learning Models Resistant to Adversarial Attacks
- CARLA simulator
- DACON
- TensorFlow Object Detection Model Build
- paper review
- 개발흐름
- Docker
- 사회초년생 추천독서
- TensorFlow Object Detection Error
- TensorFlow Object Detection 사용예시
- 기능과 역할
- Git
Archives
- Today
- Total
JSP's Deep learning
[Paper Review - AI Security] 2. Towards Evaluating the Robustness of Neural Networks 본문
Paper Review/AI Security
[Paper Review - AI Security] 2. Towards Evaluating the Robustness of Neural Networks
_JSP_ 2023. 1. 23. 20:05
1. 요약
-
“C & W(Carlini & Wagner) Attack” 라는 강력한 Targeted White-Box Attack을 소개한다.
-
C & W Attack은 Defensive Distillation을 무력화 시킨다.
-
C & W Attack은 Distance method에 따라 L_0, L_2, L_∞ 3가지 방법이 존재한다.
2. 용어 정리
1) Transferability

-
Adversarial example을 생성한 Model외의 다른 Model에도 High-Confidence로 Attack이 적용되는 것
3. Background
1) Neural Networks and Notation
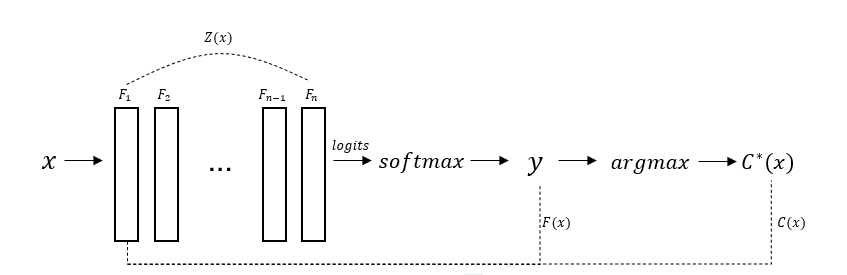
- Neural Network의 수식적 정의

2) Adversarial Examples
-
Adversarial Examples의 수식적 정의

-
Adversarial Examples의 목적
-
x와 x′ 의 distance ↓
-
C(x′ )=t의 probability ↑
-
즉, Adversarial Perturbation의 크기는 줄이고(눈에 띄지 않게), target class로 분류되는 confidence는 높이는 것
-
-
Targeted Attack의 3가지 접근법
-
Average Case
-
정답이 아닌 class 중 Random으로 target class 선정
-
-
Best Case
-
정답이 아닌 class 중 가장 공격하기 쉬운 class을 target class로 선정
-
-
Worst Case
-
정답이 아닌 class 중 가장 공격하기 어려운 class을 target class로 선정
-
-
3) Distance Metrics
-
x와 x′ 간의 거리를 계산(Distance가 0에 가까울수록 구별 불가능)
-
Distance Metrics에 따라서 생성되는 Adversarial perturbation이 달라진다.
-
본문에서는 L_0, L_2, L_∞ 3가지 Distance Metrics에 대해서 다룬다.
-
Distance Metrics 정의

4) Defensive Distillation
-
Adversarial Example에 대한 방어 기법(2017년 당시 우수한 기법)
- 수행방법
-
일반적인 방법으로 Model 학습을 진행한다.
-
학습시킨 Model로 이미지에 대한 Output을 구한다.
- 해당 output을 새로운 모델의 training label로 사용한다.
-
- 특성
-
기존의 Softmax을 smooth-Softmax로 만든다.
-
Model의 Overfitting을 방지한다. -> “blind spot”을 제거
- Model의 Gradient을 숨기는 효과가 있다. (White-Box Attack에 대한 방어효과)
-
- 한계점
- Defensive Distillation은 Non-linear neural network에 존재하는 “blind spot”을 제거하여 Adversarial Example에 대한 Resistant가 있다고 주장했으나, 실제로 FGSM에 대한 논문에서 Adversarial Example은 Non-linear한 특성 때문이 아닌 Linear한 특성 때문에 생기기 때문에 Defensive Distillation은 Adversarial Example을 제거하지 못한다.
4. Attack Algorithms
1) L-BFGS(Limited memory-Broyden-Fletcher-Goldfarb-Shanno)
-
Adversarial Examples을 생성하는 Algorithms
-
Objective function
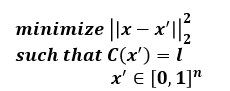
-
Objective function for solving problem

- Objective function 해석
-
x와 x′의 Distance ↓
-
x′ 의 target label loss ↓
-
2) FGSM(Fast Gradient Sign Method)
-
Sign Function을 이용하여 Adversarial Example을 생성하는 Attack 기법
-
한번의 미분으로 Attack을 수행하기 때문에 빠르게 동작하는 특징이 있다.
-
Objective function

-
모든 pixel에 대해서 target label의 loss에 sign(w) 수행한 값을 ϵ만큼 변형
-
한번의 미분으로 빠르게 동작하지만, 최적의 Adversarial perturbation을 생성하는 것은 아니다.
3) Iterative FGSM(Iterative Fast Gradient Sign Method)
- 기존 FGSM을 개선한 방법으로 FGSM에 비해서 성능이 우수
- Objective funtion

- 빈 perturbation에서 시작 -> α step만큼 반복적으로 수행 -> 최종 perturbation 생성
4) JSMA(Jacobian-based Saliency Map Attack)
- Saliency map을 이용하여 Attack을 수행하는 기법(L_0 Distance 사용)
-
모든 pixel 중 target으로의 Classification에 가장 큰 영향을 Pixel을 선택해서 변형시킨다.
-
Pixel 선택 수식

-
JSMA의 종류
-
JSMA-Z : Gradient 계산 시 logits 값을 기준으로 계산
-
JSMA-F : Gradient 계산 시 Softmax 값을 기준으로 계산
-
5) Deepfool
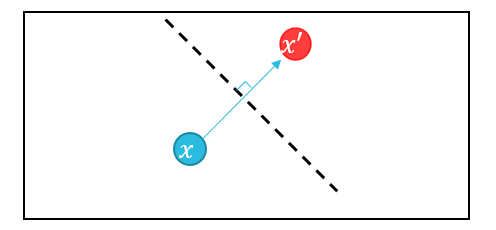
-
Untargeted Attack 기법(L_2 Distance 사용)
-
전체적으로 Linear한 Model에 대해서 적용
-
x에 대해서 Decision boundary을 넘어가도록 Projection을 수행하여 Adversarial Example을 생성한다.
-
실제 Model은 non-linear 이므로 process을 반복 수행.
-
Misclassification이 수행되면 Process 종료.
-
5. C&W Attack(Carlini & Wagner Attack)의 접근법
C&W Attack에 대한 함수를 정의하기 위한 접근방법
1) Objective function
-
f function for solving problem

-
주요 f function

- 본 논문에서는 실험적 방법을 통해서 가장 효과가 좋은 두 함수를 선정하였다.
-
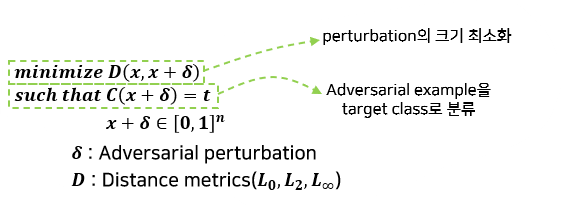
제약조건이 포함된 Objective function
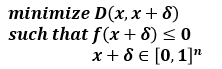
-
제약조건이 포함된 Objective function for solving problem

- target class에 대한 loss도 낮추면서 perturbation의 크기도 작게 하는 것이 목적
2) Box constraints
-
본 논문에서는 Image Normalization을 가정했기 때문에, 0≤x_i+δ_i≤1의 Box constraints가 적용된다.
- Box constraints 적용을 위한 방법
-
Projected Gradient Descent(PGD)
-
Clipped Gradient Descent
-
Change Of Variables : C&W Attack은 Change Of Variables 방법을 사용하여 Box constraints을 적용하였다.
-
(1) Projected Gradient Descent(PGD)

- 수행방법
-
Standard gradient descent로 1-step 진행
-
이후 x′의 coordinates을 box 내부로 clips
-
(2) Clipped Gradient Descent
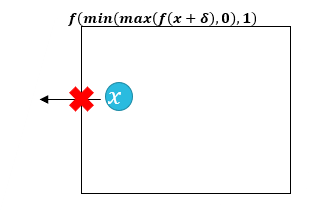
- Iteration마다 x를 clipping하지 않고, object function 내에서 clipping을 진행(즉, 수식적으로 제약)
-
f(x+δ)⇒f(min(max(f(x+δ),0),1) 의 식을 통해서 Box constraints을 적용한다.
- Projected Gradient Descent의 단점을 보완하지만, x_i가 허용된 최대치보다 커져서 Gradient descent가 flat spot에서 멈출 수 있다.
(3) Change Of Variables
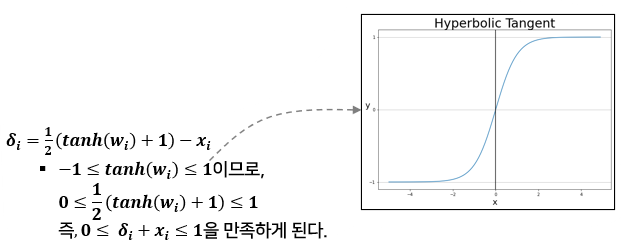
-
PGD에 비해서 smooth한 방법을 취하기 때문에 더 강력한 Adversarial perturbation이 생성될 수 있다.
- +@
-
C&W Attack에서는 Optimizer로 Adam을 사용한다.(실험적으로 가장 성능이 좋은 것 선택) – 대체적으로 빠르고 효율적.
-
실제 Image는 [0,255]의 값을 갖기 때문에 Perturbation에 대해서 변환과정이 필요한데, 이 과정은 성능에 결정적인 영향은 끼치지 않으며, CW Attack 기법은 Perturbation의 크기를 작게 하는 것이므로 이러한 사항이 고려되어서 설계되었다.
-
6. Three Attacks
- Distance Methods에 따른 3가지 C&W Attack 기법
-
각각의 Distance metrics로 만들어지는 Adversarial Examples은 서로 다르며, 각 Distance metrics로 생성된 Adversarial Examples마다 장단점이 존재한다.
-
C&W Attack은 Distance metrics(L_0, L_2, L_∞)에 따라서 총 3가지가 존재한다.

1) L0 Attack

- L0 Distance 수식

- 변화된 Pixel의 개수로 측정하는 방법
- 수행방법
- L2 Distance을 이용하여 Classification에 큰 영향을 미치지 않는 pixel 선택 및 고정(고정된 pixel의 값은 바뀌지 않는다)
-
그 외의 pixel의 값을 변화시키면서 Adversarial perturbation 생성
-
원하는 Adversarial perturbation을 생성할 때까지 ‘2)’을 반복한다.
- 특징
-
특정 Pixel을 크게 변화시키기 때문에 Perturbation이 눈에 띄는 경향이 있다.
-
2) L2 Attack
- L2 Distance 수식

- L2 Attack 수식
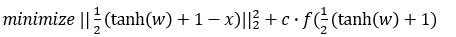
- L2 Attack에 사용된 f function(f6)
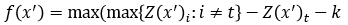
-
k : Target t에 대한 Adversarial Example의 confidence을 조정
(k↑ : target t의 logits↑(High-confidence) ) -
평가 시에는 k=0으로 설정
- 특징
-
Multiple random starting points 사용시
-
다양한 위치(random pixel)에서 Perturbation 생성
-
더 강력한 Adversarial Example 생성
-
이미지의 왜곡을 높이는 단점도 존재
-
-
Original Image와 Adversarial Image의 구분이 잘 되지 않는다.
-
3) L∞ Attack
- L∞ Distance 수식

- L∞ Attack 수식
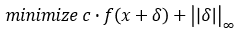
- 문제점
-
미분 불가능 -> 최적화 불가능
-
“가장 큰 값”에 대해서만 Penalty 부여 -> 크기가 작은 축에 대해서는 크게 영향을 주지 못한다.
-
- L∞ Attack 수식 개선

-
가장 큰 값만이 아닌 큰 값에 대해서 Penalty 부여 -> 값이 상대적으로 작은 축에 대해서도 고려한다.
4) C&W Attack의 특징
-
기존 Attack에 비해 Model에 대한 공격 성공률이 높다.
-
L0, L2 Attack을 사용하면 기존의 Attack보다 더 작은 Perturbation을 생성한다.
-
L∞는 iterative gradient descent보다는 성능이 떨어진다.
7. Defensive Distillation
1) 정의
- 수식
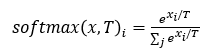
- 수행방법
- Teacher model과 distilled을 수행할 model을 같은 사이즈로 준비
-
Distillation temperature(T)을 높게 설정
-
학습진행
- 수행단계
-
teacher network 학습
-
teacher network의 Output을 soft label로 사용
-
soft label을 distilled을 적용할 network의 label로 사용하여 학습
-
distilled network을 배포하여 사용할 때는 Temperature(T)의 값을 1로 하여서 사용
-
- 특징
-
Temperature을 조절하여 Model의 Gradient 값을 숨기는 효과가 있다.
-
Logits 값을 T배로 증가시키는 특징이 있다.
-
2) 적용 예시
- 학습 : Temperature(T) = 100
-
배포 : Temperature(T) = 1
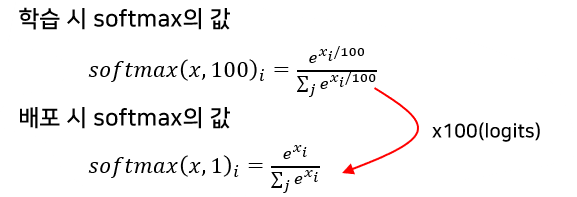
-
결론적으로, 학습 시 softmax의 가장 큰 logits 값이 매우 커지게 되고 다른 값들은 매우 작아지게 된다. => Gradient을 숨기는 효과가 있다.
-
하지만 C&W Attack은 white-box attack이므로 T값에 대해서 알고 있다고 가정하면
F′ (x)=softmax(Z(x)/T)의 수식을 통해서 본래 logits 값으로 되돌릴 수 있다. -
결국 Adversarial example에 대해서 취약하게 된다.
3) C&W Attack 외의 다른 Attack에 적용한 결과
(1) L-BFGS & Deepfool & JSMA-F

(2) JSMA-Z
-
Gradient Vanishing 문제는 없다. => logits 값을 이용하기 때문
-
하지만, T의 값에 따라 logits이 그 배율만큼 커지기 때문에 JSMA-Z을 통한 logits 값의 변화는 Model의 classification에 있어서 큰 영향을 주지 못해서 실패하게 된다.
(JSMA-Z에서는 logits의 변화량을 기준으로 중요 pixel을 선정한다)
(3) FGSM
-
Gradient가 대부분 0인 문제 발생(Gradient vanishing)
-
F′ (x)=softmax(Z(x)/T) 을 적용해도 Distillation을 무력화 시키지 못한다.
8. 실험
1) c 값을 이용한 Adversarial Example 변화
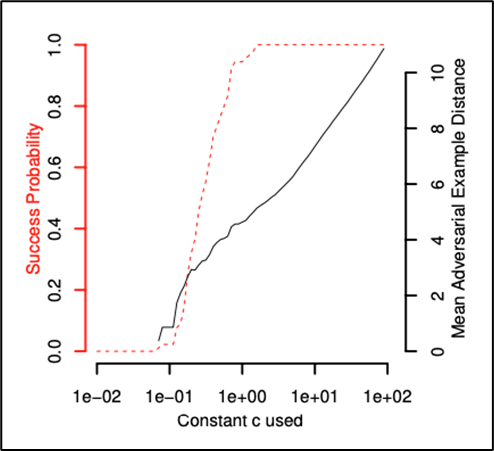
-
c 값을 이용한 Adversarial Example 조정 (L2 distance로 실험)
- MNIST dataset을 통한 실험에서 측정
- D(x, x+δ)+c⋅f(x+δ) 의 c 값 변화에 따른 Success prob vs. Mean avg Distance
(Distance가 크다는 것은 x에 대해서 x′의 왜곡이 심하다는 것. 즉, Perturbation의 크기가 크다는 것) -
c↑ : perturbation 크기 ↑ Success prob ↑(trade-off 관계)
2) f1 ~ f7 성능 실험
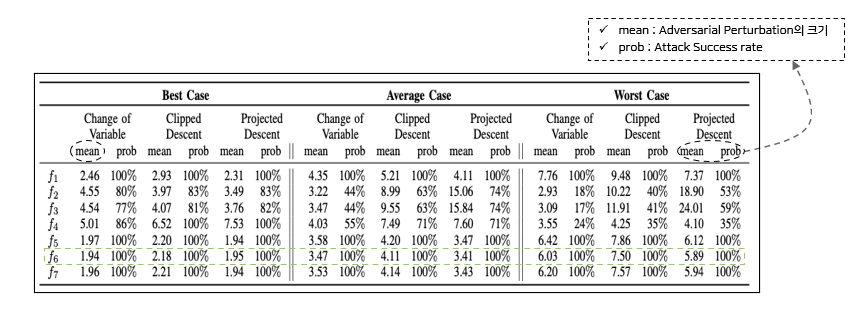
-
Attack Success rate가 100%이 아닌 f function에 대해서는 성공한 경우의 Perturbation에 대해서만 계산
-
결론적으로, f6 function이 가장 성능이 좋았기 때문에 C&W Attack에 사용했다.
3) Distance Methods 마다 생성하는 Perturbation 확인

-
All black or All white 이미지에 대해서도 perturbation이 생성된다.
-
L0 Attack으로 생성된 perturbation이 눈에 띄는 경향이 있다.
-
각 Attack마다 생성하는 perturbation이 다르다 => 그런데도 같은 Target class로 오분류 시킴
4) 다른 Attacks과 C&W Attack 성능 비교(MNIST, CIFAR dataset 사용)

-
L0, L2를 사용하는 Attack 기법에서는 C&W Attack이 우수하다.
- L∞를 사용하는 Attack 기법에서는 Iterative Gradient Sign Attack이 더 우수하다.
(더 빠르고 성능도 좋음)
5) 다른 Attacks과 C&W Attack 성능 비교(ImageNet : 좀 더 복잡한 dataset)
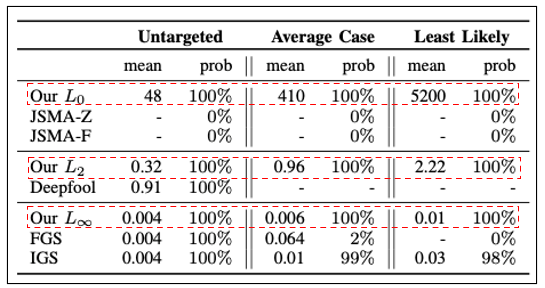
-
C&W L0은 공격 성공률은 좋지만, perturbation의 크기가 매우 커진다.
-
C&W L2은 Deepfool에 비해 성능이 좋다.
-
C&W L∞도 성능이 좋다.
-
C&W Attack은 다른 Attacks보다 성능은 좋지만 속도면에서는 뒤쳐진다.
6) Distilled Network에 대한 C&W Attack 성능 검증(MNIST, CIFAR)
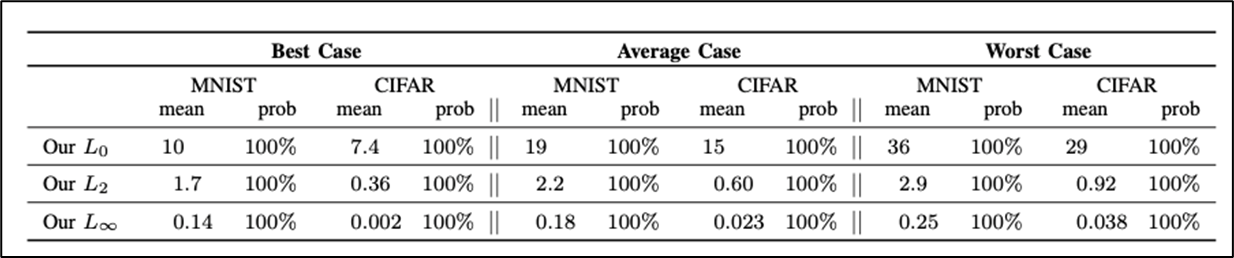
-
prob가 100%으로 Defensive Distillation을 아예 무력화 + Perturbation의 크기도 작다.
7) Distilled Network에 대한 C&W Attack 성능 검증(MNIST, CIFAR) - T, K 값 변경

-
Temperature의 값을 변경해도 C&W Attack에 여전히 취약하다.
-
K의 값을 크게 할수록 전이공격에 대한 성공률이 높아진다.
9. 요약
-
C&W Attack은 Model의 Parameters을 모두 알고 있는 White-box Targeted Attack으로 Defensive distillation을 무력화시키는 강력한 공격 기법이다.
-
C&W Attack는 Distance Methods에 따라 3가지 공격법이 존재하며 각각의 특징이 존재한다.
-
C&W Attack에서 clean image와 adversarial image의 distance와 Attack success prob은 trade-off 관계가 있다.
Comments


