[Paper Review - AI Security] 3. Towards Deep Learning Models Resistant to Adversarial Attacks

1. 요약

①“Optimization 관점”에서 Adversarial Robustness 정의
(=> 강력한 Adversarial Attack에 대한 Defense을 학습)

②Adversarial Training with Strong Attack => Robustness↑

③ Model’s Capacity↑=> 복잡하고 정교한 Decision boundary => Robustness↑

④복잡한 Dataset에 대한 Attack에 대해서는 Defense 성능이 좋지 못하다.

 

2. 용어 정리

 

1)“First-Order Attack”

“한 번의 미분”만으로 공격을 수행하는 기법(Loss function에 대해서 한 번) => 즉, 오차역전파를 한번만 수행함.

PGD(Projected Gradient Descent), FGSM(First Gradient Sign Methods) 등의 기법이 존재한다.

본 논문에서는 가장 강력한 Attack 기법으로 PGD을 채택하여 사용한다.

 

2) “Saddle point problem”

• Defensive와 Attack을 동시에 다루는 문제
• Min-Max problem에서 Saddle point(최적의 점)로 수렴하도록 하는 것
• Saddle point problem
  • Inner Maximization problem
    • Loss을 최대로 하는 Adversarial Examples을 만드는 문제(Attack)
  • Outer Minimization problem
    • Adversarial Examples에 대한 loss을 최소화하는 문제(Defense)

 

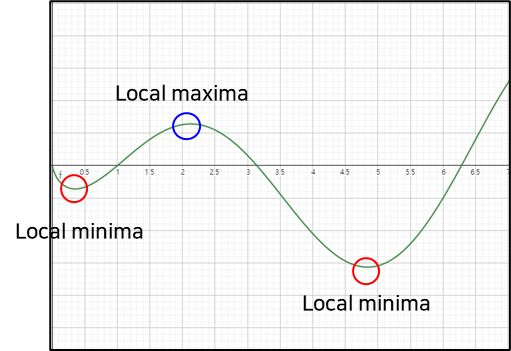
3) “Non-convexity & Non-concavity”

• Non-convexity
  • 여러 개의 지역 최저점(Local minima)을 갖는 함수
• Non-concavity
  • 여러 개의 지역 최대점(Local maxima)을 갖는 함수
• Gradient Descent을 시작하는 위치에 따라서 수렴 결과가 달라진다.

[출처] https://skyil.tistory.com/33

 

4) “Empirical Risk Minimization(ERM)”

• 주어진 한정된 학습 데이터의 분포를 따르는 Loss function의 기댓값을 최소화 시키는 과정

[출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

 

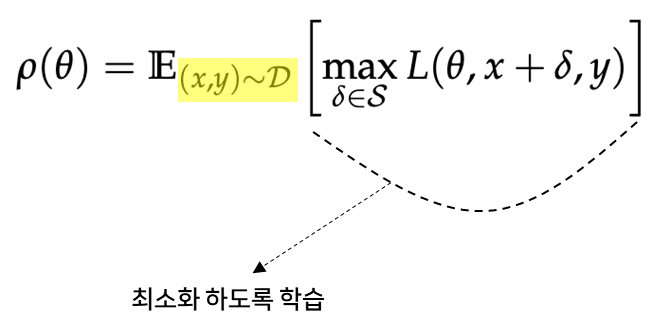
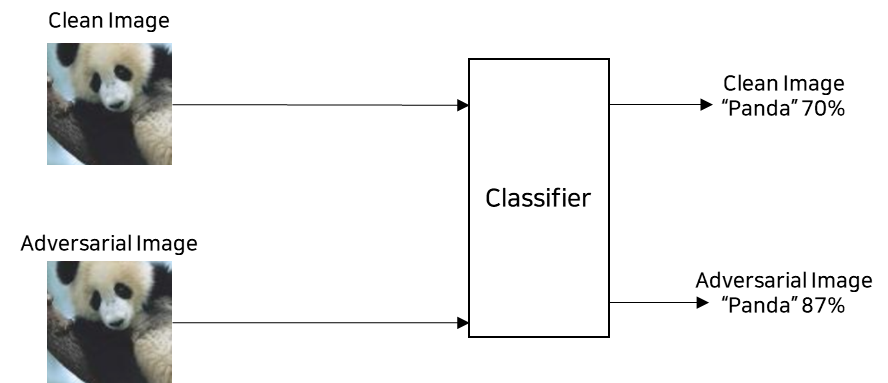
5) “Label leaking”

• Adversarial Training을 적용했을 때, Adversarial example의 validation loss가 Natural example loss보다 낮은 경우
• 즉, Classification Model이 Natural example보다 Adversarial example을 더 잘 분류하는 현상

 

3. 최적화 관점에서의 적대적 공격과 방어

 

1) 수식

 

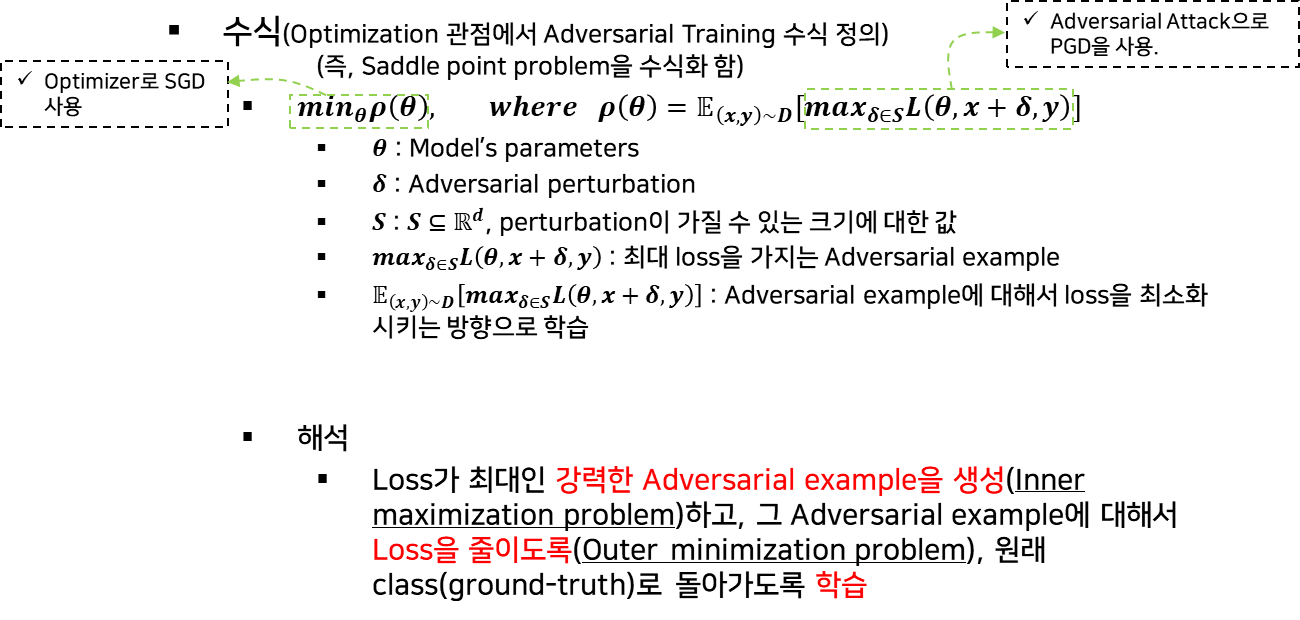
2) 적대적 공격과 방어의 통합적 관점

 

(1) 공격

• 기본 수식 정의

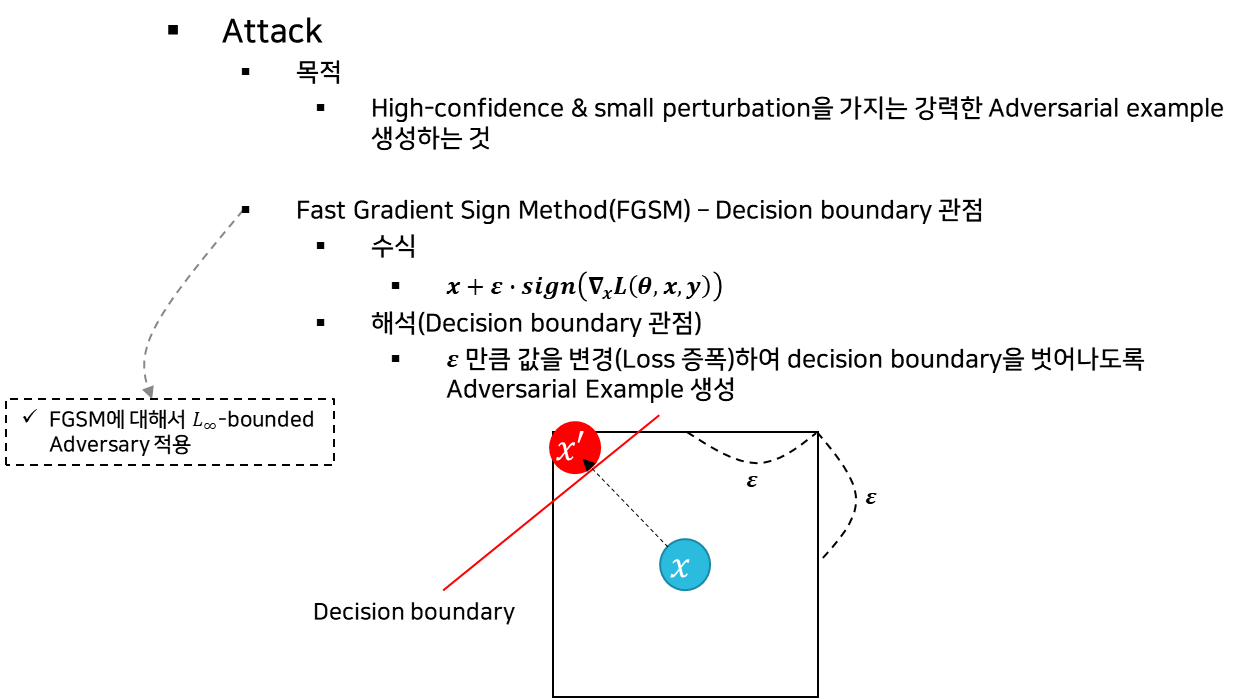
• PGD 수식 정의

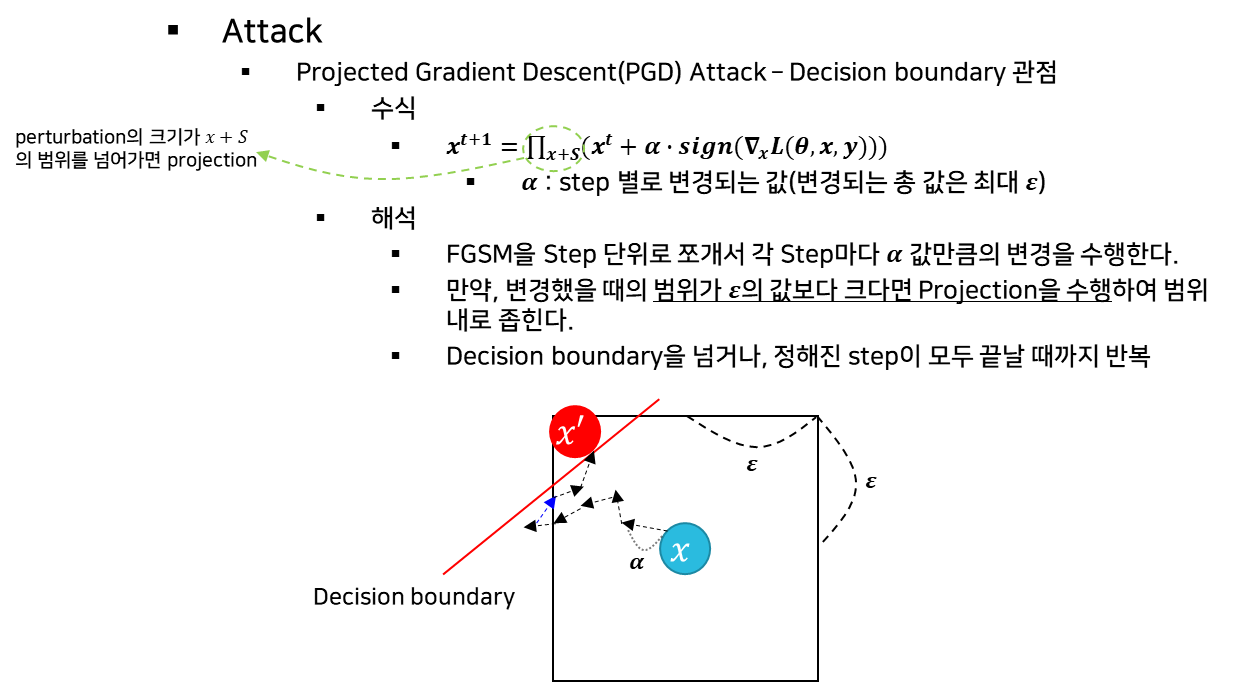
(2) 방어

• 목적
  • Adversarial을 찾기 어렵게 하거나, 아예 존재하지 않게 만드는 것
    => Constraints box을 고려해서 Decision boundary을 복잡하고 정교하게 만든다.

 

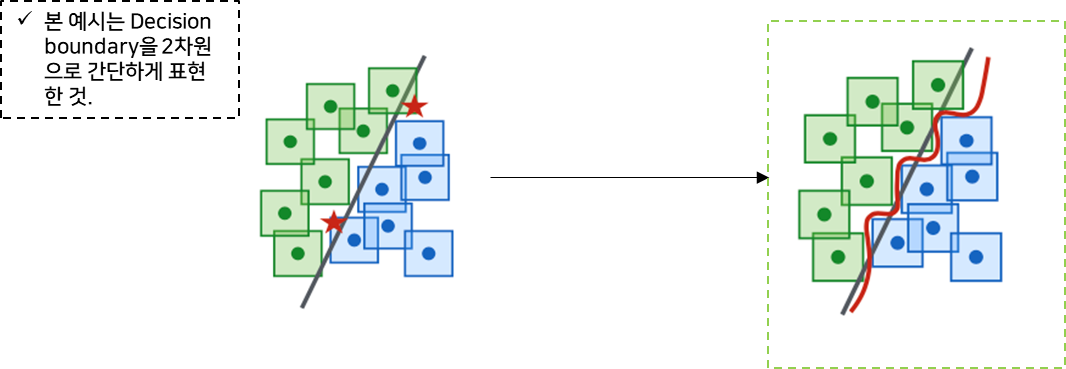
4. 범용적 강건성

 

1) Adversarial Training

 

(1) Adversarial Training vs. Standard Training

 

A. 학습 방법 및 데이터 셋에 따른 오차 값 측정

[출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

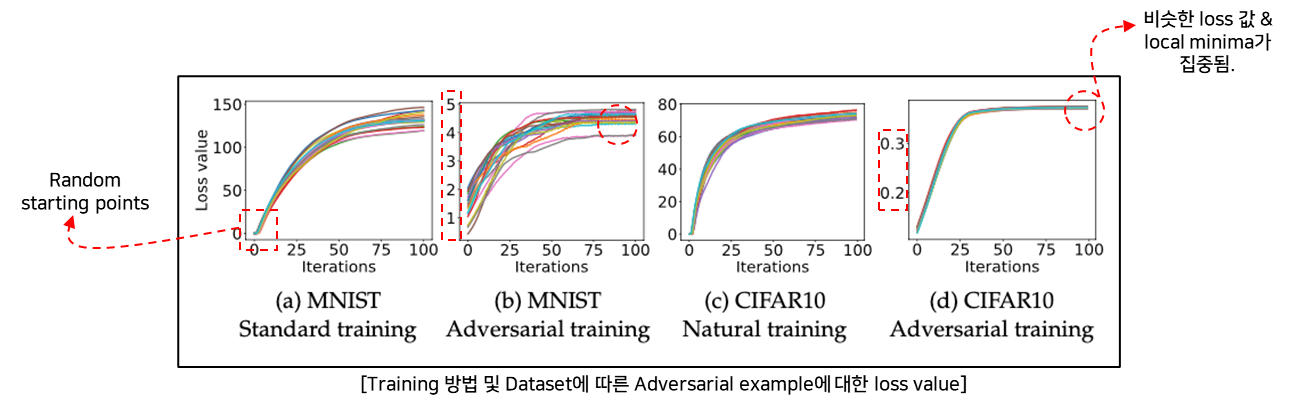
• 실험
  • Dataset : MNIST, CIFAR10
  • Starting points : Random points(20회)
  • Attack method : PGD Attack
• 결과
  • Random starting points에서도 Adversarial Training을 적용한 학습이 잘됨.
    (Saddle point problem에 대해서 잘 학습한다.)

B. 학습 방법 및 데이터 셋에 따른 오차 값 분포 측정

[출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

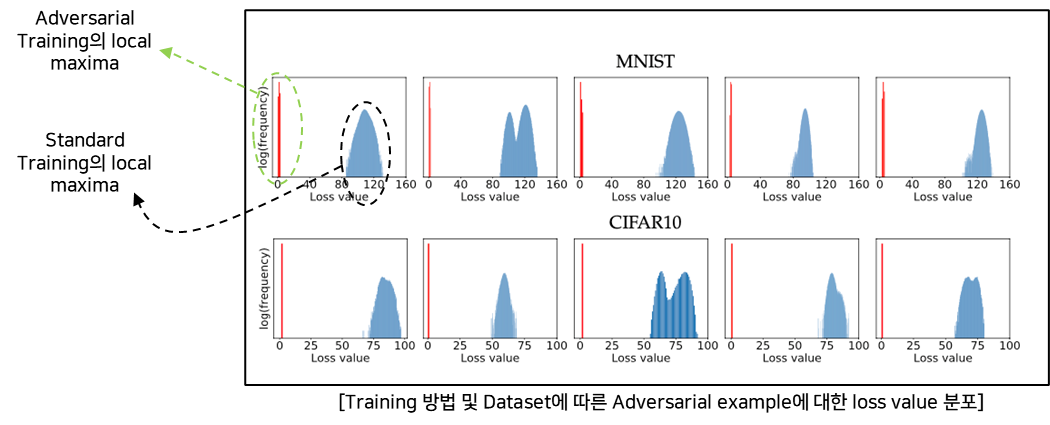
• 실험
  • Dataset : MNIST, CIFAR10 (5 examples – evaluation dataset)
  • Starting points : Random starting points(10^5)
  • loss : cross entropy loss
• 결과
  • Adversarial Training은 MNIST & CIFAR10에 대해서 잘 학습된다.

 

2) Fisrt-Order Adversaries

한번의 오차 역전파를 통해서 공격하는 방법 중 가장 강력한 공격기법으로 적대적 학습을 한다면 범용적 강건성을 추구할 수 있을 것

• Adversarial Training 수식

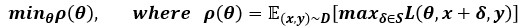
• 결국, max_(δ∈S) L(θ,x+δ,y)에서 성능이 좋은 Attack을 사용하면 그만큼 Defense의 성능도 좋아지게 된다.
• 예시) Attack 성능 : A1 > A2 > A3 > A4 > A5 (similar mechanisms)

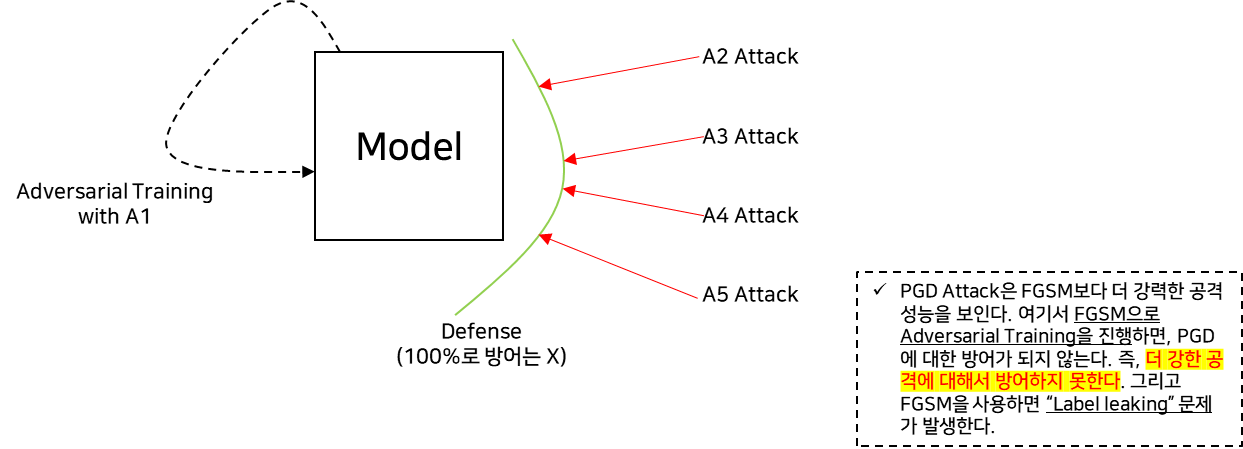
다른 공격기법에 대한 모델의 성능 측정

=> first-order attack에서 PGD가 “universal” attack으로 적합하다. (즉, 가장 강력하다)

 

3) Saddle point problem 해결

[이미지 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

 

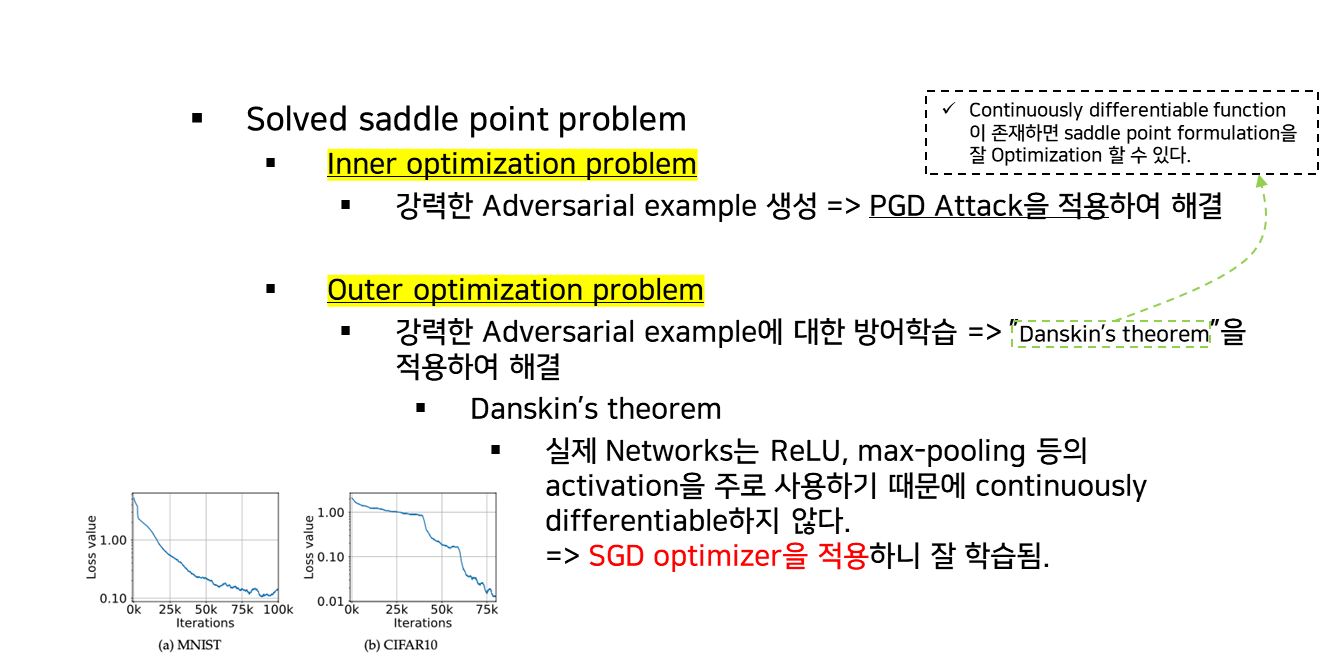
5. 모델의 크기와 강건성과의 관계

 

1) Decision boundary 관점에서의 강건성

[이미지 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

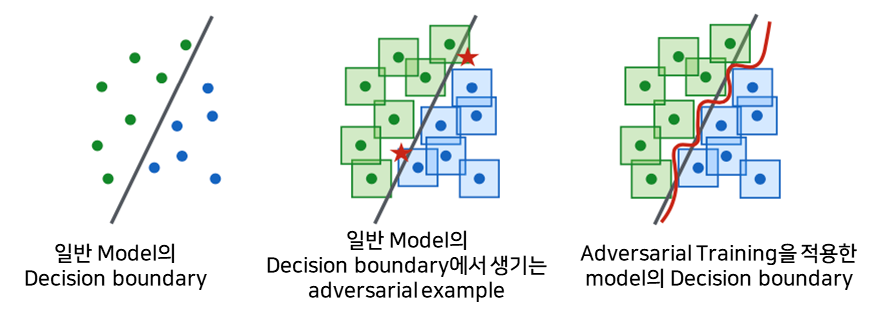
• Decision boundary가 constraint box을 고려해서 좀 더 정교하고 복잡하게 형성됨. (즉, 모델의 크기가 클수록/정교할 수록 강건성이 커진다)
• Adversarial Example의 생성 자체를 막거나, 어렵게 한다.

 

2) 정리

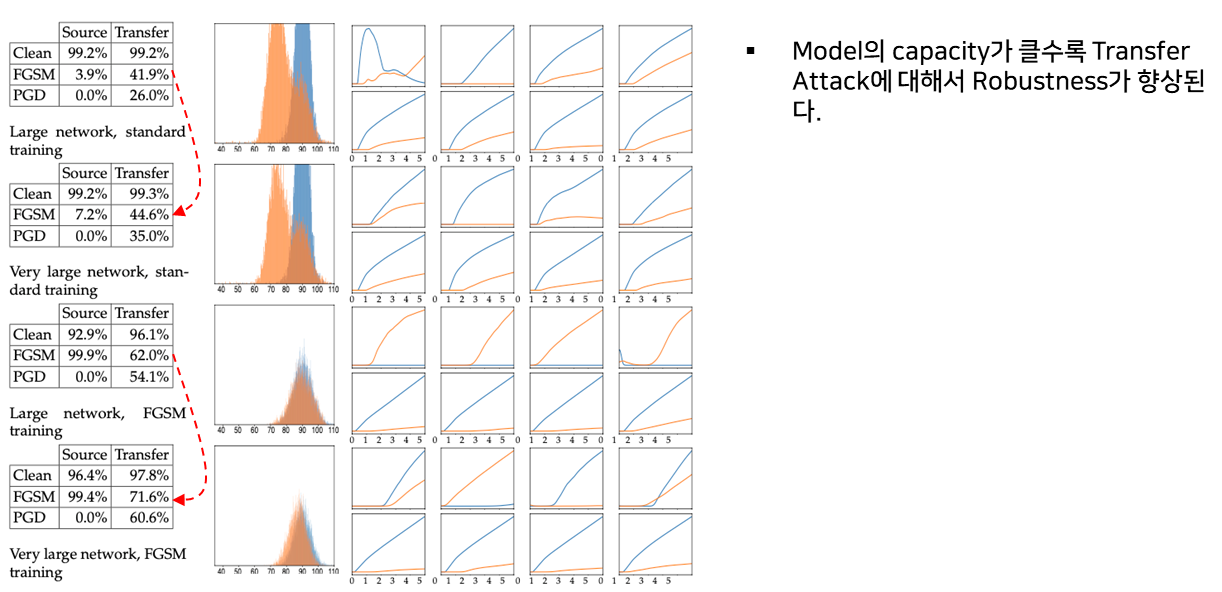
• Model의 Capacity가 클수록 Model의 Robustness도 향상된다.
  (perturbation의 크기가 작을수록 더 효과적)
• Capacity는 Adversarial Training의 성능에도 영향을 미친다.
  (Capacity가 작으면 “Label leaking” 문제를 야기)
• Capacity을 늘리고 더 강한 Attack을 Adversarial Training에 적용하면 Transfer Attack에 대한 Robustness도 향상된다.
  

 

6. 실험

 

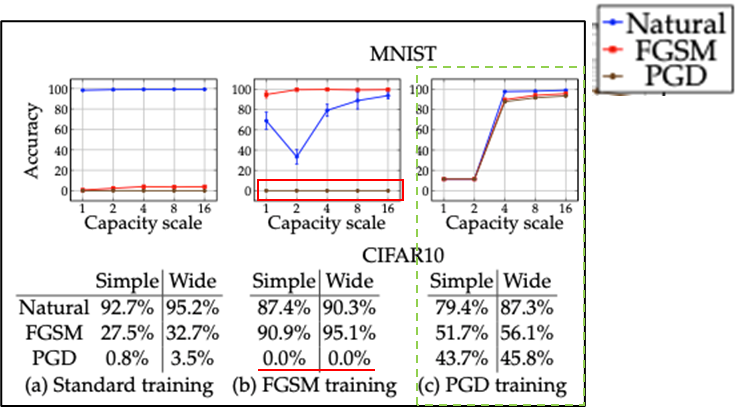
A. 모델의 크기에 따른 적대적 학습을 통한 모델의 강건성 측정

[이미지 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

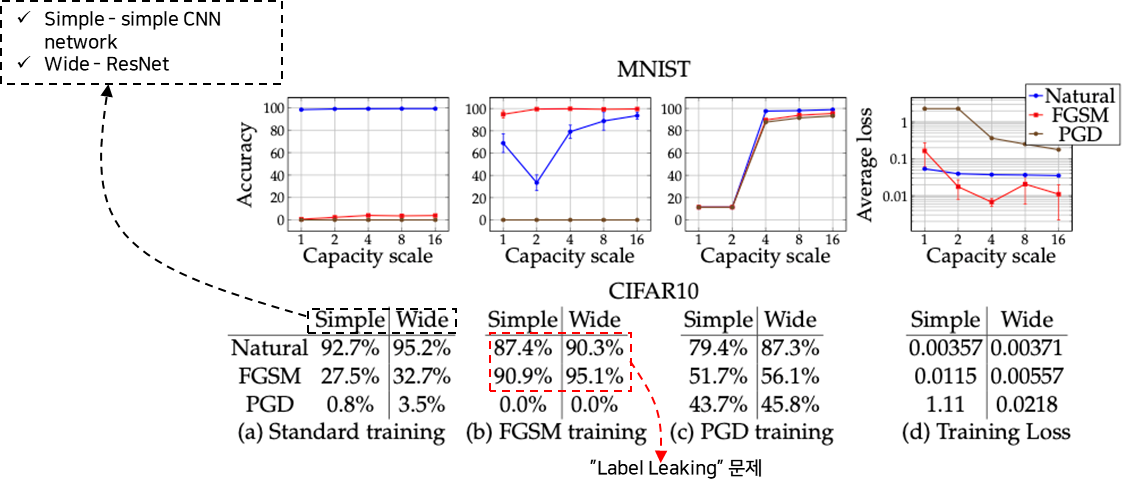
• 모델의 크기↑
  • Adversarial example에 대한 accuracy↑loss↓
• 약한 공격 기법을 통한 학습
  • Label Leaking 문제 발생
  • 더 강한 공격 기법에 대해서 방어하지 못함.

 

B. MNIST & CIFAR10 데이터 셋에 대한 실험

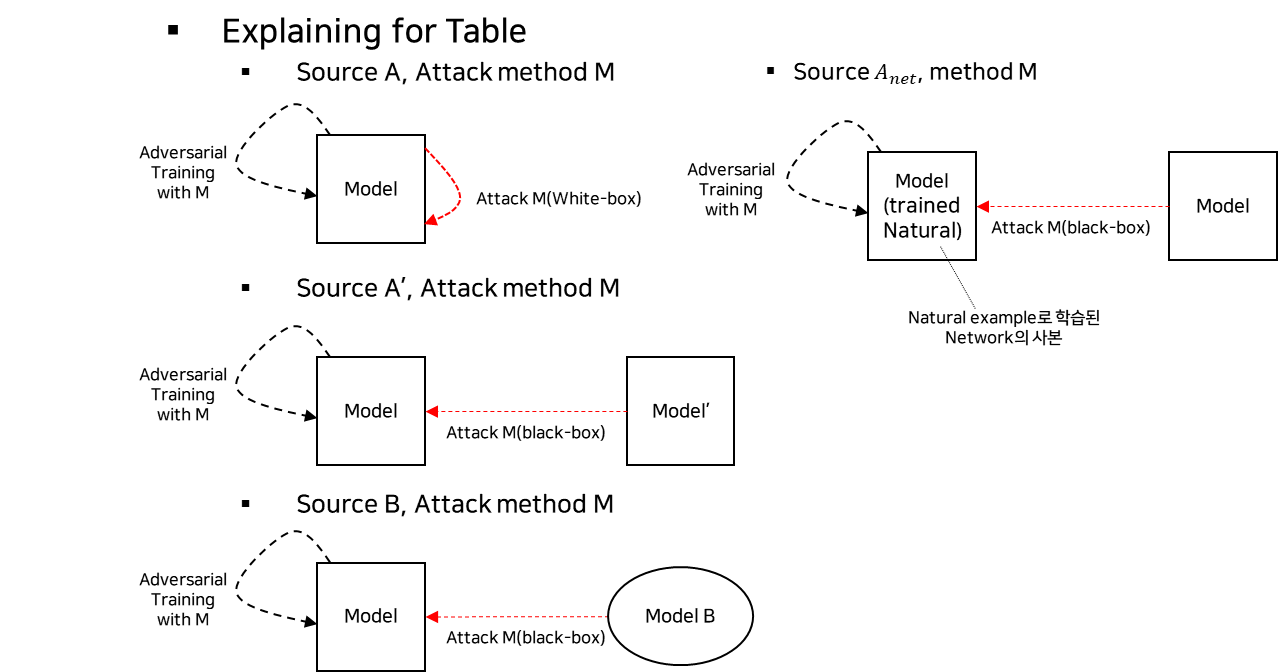
• 실험전 초기 설정 및 정의

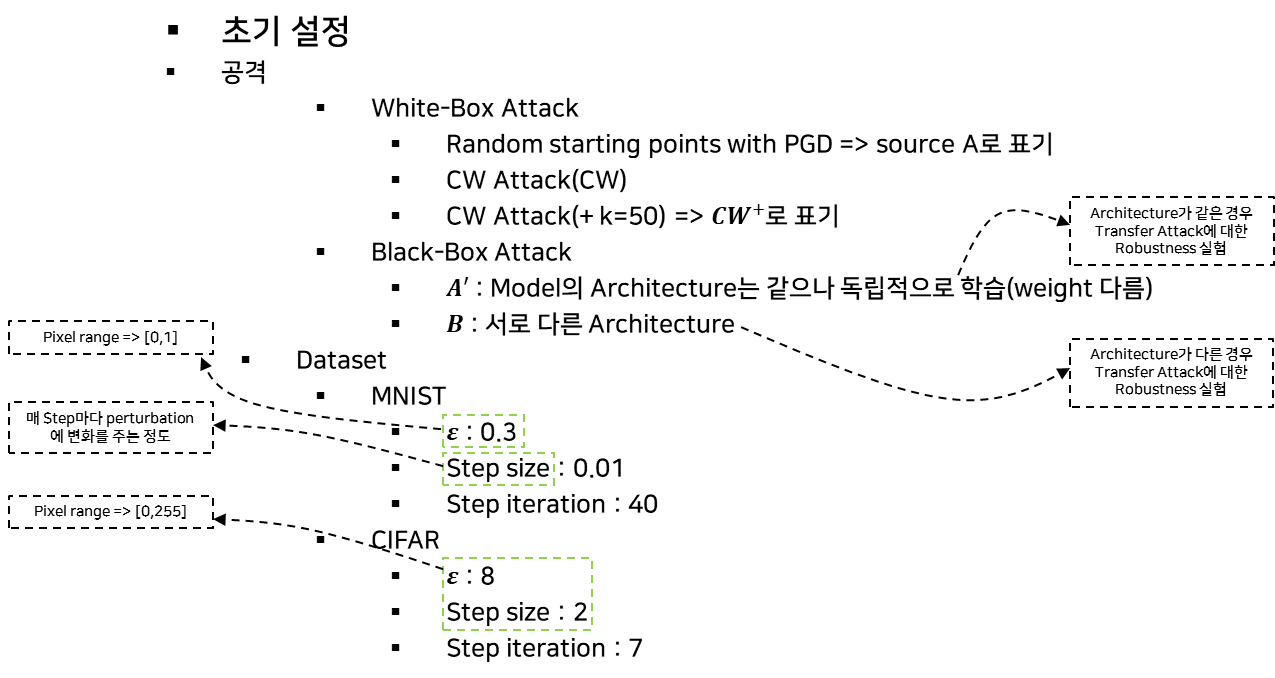
• 실험 결과 표 용어정리

 

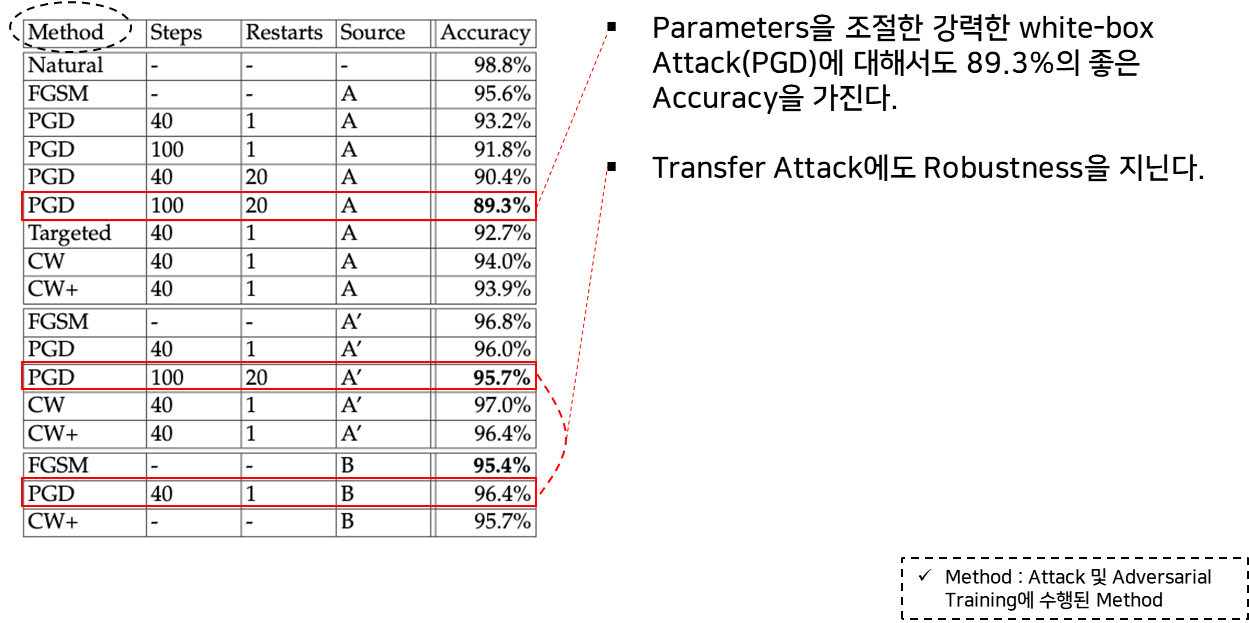
MNIST 데이터 셋에 대한 성능 실험

[표 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

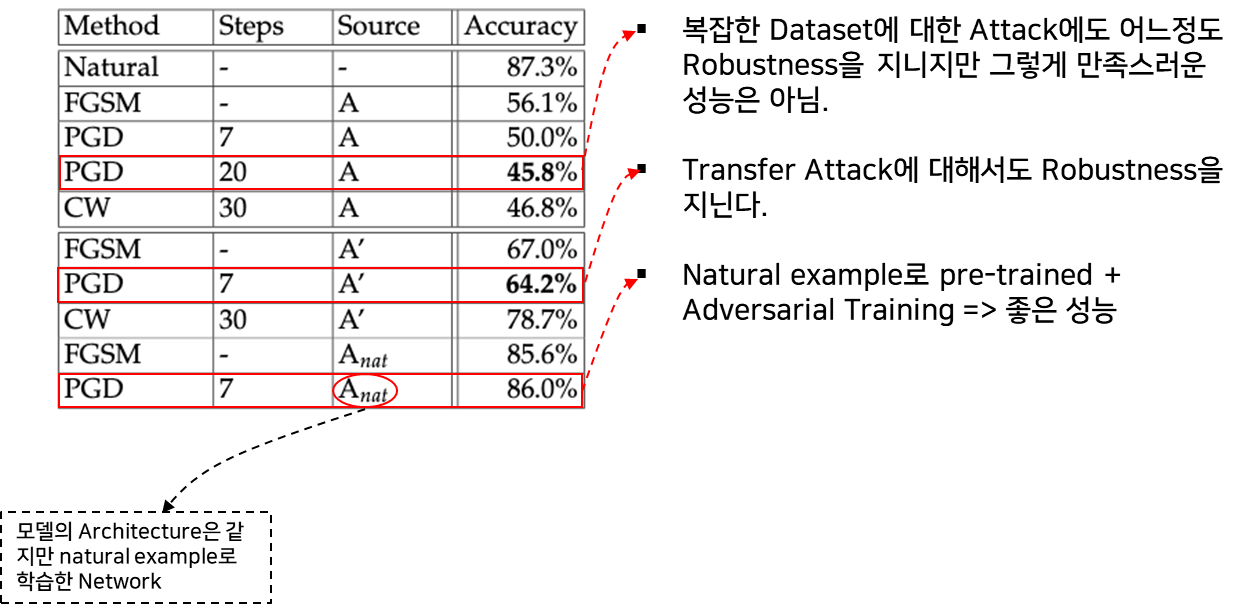
CIFAR10 데이터 셋에 대한 성능 실험

[표 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

 

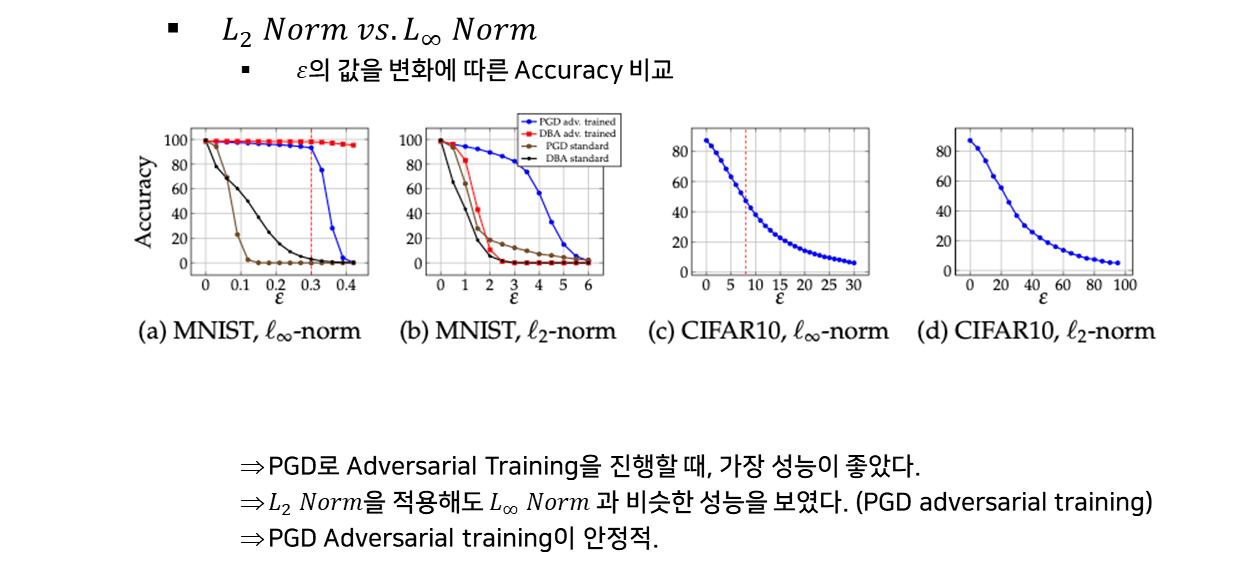
Distance Method 변화에 따른 실험

[이미지 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

 

모델의 크기에 따른 전이성과 강건성 실험

[이미지 출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

 

L2 Distance method을 사용했을 때, 결과 시각화

[출처] Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

• L2 Norm bounded attack은 사람이 보기에도 잘못 분류할 수 있도록 Perturbation을 생성하는 경향이 있다.

 

@ 본문에서 제시한 적대적 학습에 대한 생각

• Min-Max problem을 적용하여 가장 강력한 Attack에 대한 방어를 학습하는 기법. 즉, Adversarial Example에 대한 feature을 잘 학습.
• 장점
  • 현재 공개된 Attack 기법으로는 무력화할 수 없다.
• 한계점
  • Attack 기법을 모르면 Adversarial Training을 적용할 수 없다.
  • 더 강한 Attack에 대해서는 방어하지 못한다
  • 즉, 실제 상황에서 알지 못하는 더 강한 Attack이 적용되면 무력화된다.

 

---

[참조]

[1] Aleksander Mardry. Aleksandar Makelov. Ludwig Schmidt. Dimitris Tsipras. Adrian Vladu. Towards Deep Learning Models Resistant to Adversarial Attacks, IN ICLR, 2018.

[2] 동빈나. https://www.youtube.com/watch?v=6RBpdAC9nwY